GeoWerkstatt-Projekt des Monats März 2015
Projekt: 100 Jahre Einsteins Allgemeine Relativitätstheorie
Forschende: Franz Hofmann, Enrico Mai, Liliane Biskupek
Projektidee: Die Gültigkeit der Einsteinschen Gravitationstheorie lässt sich sehr gut mit geodätischen Methoden testen, insbesondere durch die Analyse von Lasermessungen zum Mond.
Im Jahr 1915 wurde die Formulierung der Allgemeinen Relativitätstheorie durch Albert Einstein abgeschlossen. Sie hat die Betrachtung von Raum und Zeit auf eine völlig neue Basis gestellt und zu einem neuen Verständnis der physikalischen Zusammenhänge im Großen geführt.
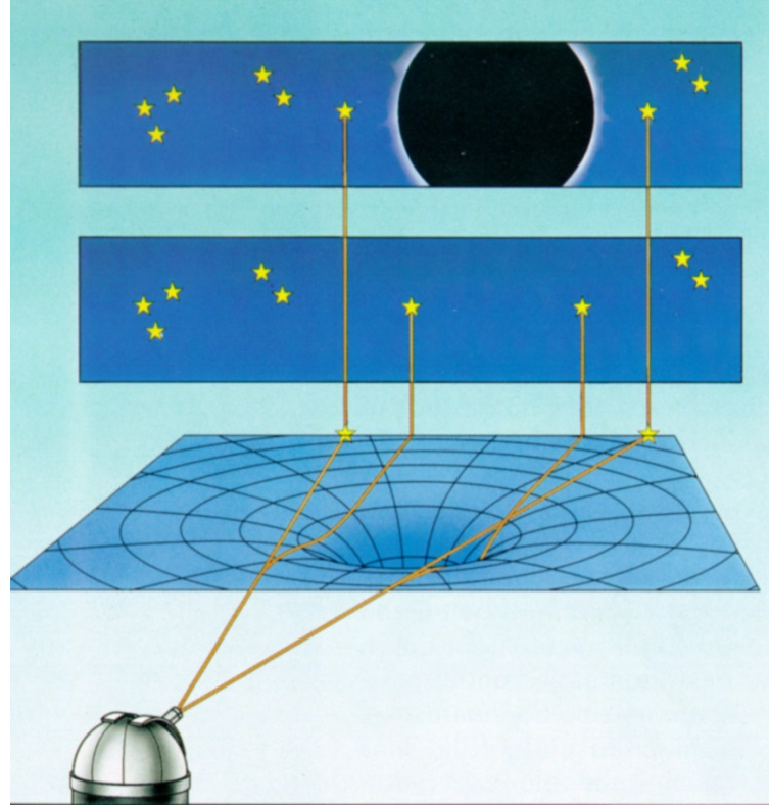
Die Gültigkeit der Relativitätstheorie wurde durch drei klassische Tests nachgewiesen (Will 1993): i) anomale Bewegung des Planeten Merkur, die so genannte Perihelanomalie mit ca. 43 Bogensekunden/Jahrhundert. Heute findet man diesen Effekt auch bei Satellitenbahnen. ii) die Lichtablenkung an massereichen Objekten, z.B. Licht von fernen Sternen am Sonnenrand mit 1,75 Bogensekunden. Lichtablenkung tritt bei allen elektromagnetischen Signalen auf, z.B. auch bei VLBI. iii) Gravitationsrotverschiebung, also die Frequenzverschiebung (von weiß zu rot) durch nahe Massen; sie spielt eine große Rolle bei der Analyse von GPS-Signalen.
Die Perihelanomalie des Merkur war vorher schon beobachtet worden und wurde durch die Einsteinsche Theorie endlich erklärt. Die Lichtablenkung am Sonnenrand wurde experimentell erstmals durch Beobachtungen bei einer Sonnenfinsternis 1919 nachgewiesen. Am 20. März 2015 soll das Experiment bei einer erneuten Sonnenfinsternis wiederholt werden. In Deutschland ist die Sonnenfinsternis nur partiell sichtbar; Interessierte können diese auf dem Geodäsie-Messdach (Nienburger Straße 1, Hannover) selbst verfolgen.
In der Geodäsie sind alle Messprozesse durch die Relativitätstheorie betroffen. Die Modellierung der geodätischen Weltraumverfahren (GNSS, VLBI, SLR/LLR) muss relativistisch erfolgen, also die zugrunde liegenden Referenzsysteme, die Signalausbreitung, die Bewegung von Satelliten und Himmelskörpern, die Messung von Abständen, Frequenzen, Zeitspannen usw. (Müller et al. 2008).








Aus den geodätischen Messungen lassen sich umgekehrt nun Vorhersagen der Relativitätstheorie untersuchen. Beispiele sind die Ablenkung von Mikrowellen an der Sonne mittels VLBI oder relativistische Rotationen von Satellitenbahnen mit SLR. Das beste Werkzeug für relativistische Tests im Sonnensystem sind aber die Abstandsmessungen zum Mond (Lunar Laser Ranging, LLR), die seit der ersten bemannten Mondlandung 1969 kontinuierlich durchgeführt und am LLR-Analysezentrum des Instituts für Erdmessung der Leibniz Universität Hannover ausgewertet werden.
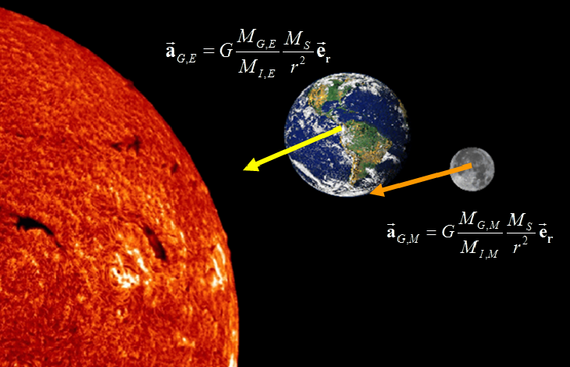
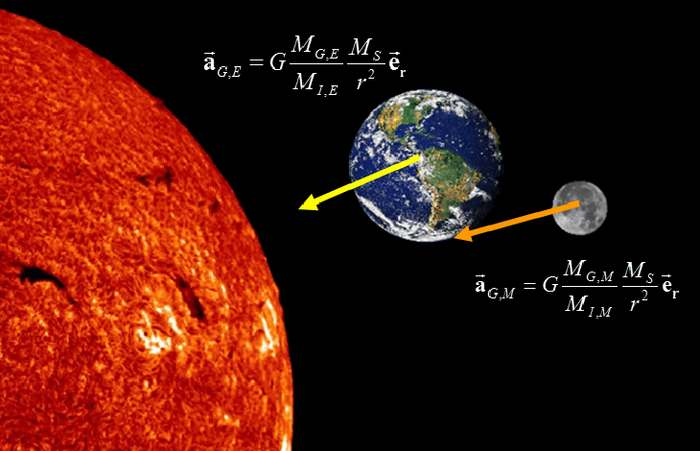
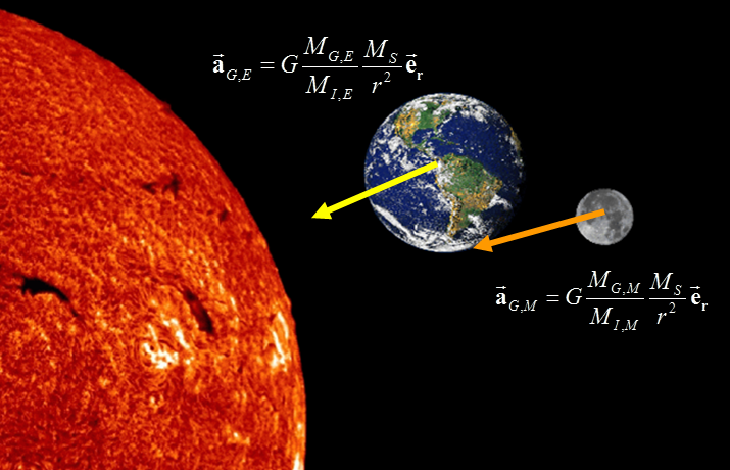
Durch den großen Erde-Mond-Abstand (im Mittel 384000 km) sind die relativistischen Effekte relativ groß. Neben metrischen Parametern, die ein Maß für die Krümmung der Raumzeit oder mögliche bevorzugte Bezugssysteme (die es bei Einstein ja nicht gibt) sind, lassen sich weitere Eckpfeiler der Einsteinschen Theorie untersuchen. Hierzu zählt die Gültigkeit des Äquivalenzprinzips, dass also alle Massen in einem Gravitationsfeld gleich beschleunigt werden. Mit LLR wird getestet, ob Erde und Mond gleichermaßen im Gravitationsfeld der Sonne fallen, was mit einer Genauigkeit von 10-13 bestätigt werden kann. In einem weiteren relativistischen Test mit LLR wird untersucht, ob die Gravitationskonstante G wirklich zeitlich konstant ist. Aus den 45 Jahren an LLR-Beobachtungen kann man eine mögliche Abweichung von der Konstanz mit einer Genauigkeit von Ġ/G< 2*10-131/Jahr einschränken. Für weitere Erläuterungen zu LLR und relativistischen Tests wird auf Müller et al. (2014) verwiesen.
Literatur
Müller, J.,Biskupek, L., Hofmann, F., Mai, E.: Lunar Laser Ranging andRelativity. Book chapter in “Frontiers of Relativistic Celestial Mechanics”, vol. 2 (ed. by S. Kopeikin), de Gruyter, p. 99-146, 2014.
Müller, J., Soffel, M., Klioner, S.: Geodesy and Relativity. Journal of Geodesy, doi 10.1007/s00190-007-0168-7, 2007, paper version: JoG, Vol. 82, No. 3, 133-145, 2008.
Will, C.M.: Theory and Experiment in GravitationalPhysics. Cambridge University Press, England,2 Aufl., 1993.


