GeoWerkstatt-Projekt des Monats Mai 2021
Projekt: Qualitätsgerechte Virtualisierung von zeitvariablen Objekträumen
Forschende: Jan Hartmann, Mohammad Omidalizarandi und Ingo Neumann
Projektidee: Verlagerung von ortsbezogenen Erfassungs-, Verwaltungs- und Geschäftsprozessen in den virtuellen Raum
Kritisch betrachtet der Bauherr die neue Wand. Tritt einen Schritt näher, schaut noch einmal genauer hin. Nickt schließlich zufrieden und verabschiedet sich kurz darauf. Die Bauleiterin setzt erleichtert die Virtual Reality-Brille ab. Alles läuft nach Plan. Die häufigen Abstimmungen mit allen Beteiligten zahlen sich aus. Auch wenn der Bauherr in München arbeitet und die Bauleiterin in Hannover. Der digitale Zwilling des neuen Hauses macht es möglich.
Solche Szenen könnten in Kürze alltäglich werden. Die Digitalisierung der Baubranche und die damit einhergehende Einführung von Bauwerksinformationsmodellen (BIM) eröffnet eine Vielzahl neuer Möglichkeiten. Mit Hilfe von Multi-Sensor-Systemen können erstmals Bauwerke und Objekte vollständig und zu jeder Zeit erfasst und dokumentiert werden. Das Ergebnis sind kolorierte 3D-Punktwolken. Sie stehen den Anwendern als authentischer digitaler Zwilling für die Betrachtung, Begutachtung und Analyse bereit.
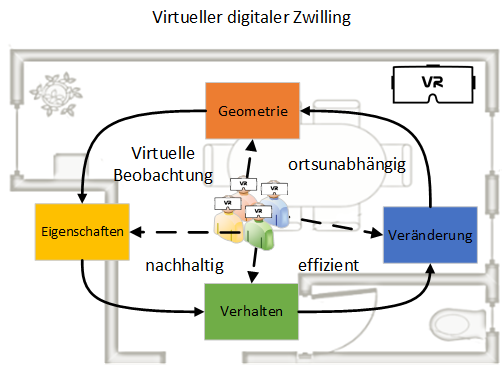
In unserem Forschungsprojekt „Qualitätsgerechte Virtualisierung von zeitvariablen Objekträumen“ (QViZO) wollen wir ein neuartiges Verfahren entwickeln, um Erfassungs-, Verwaltungs- und Geschäftsprozesse, die bisher vor Ort stattfinden mussten, in den virtuellen Raum zu verlagern. Anwender sollen orts- und zeitunabhängig auf den digitalen Zwilling zugreifen und rechtskräftige Beurteilungen treffen können. Vor-Ort-Termine sollen so signifikant reduziert werden. Die Anwender greifen auf den digitalen Zwilling per VR-Technologie (Virtual Reality) zu und können die erfassten Objekte bis ins Detail genau betrachten.

 ©
GIH
©
GIH
Doch wie genau muss der digitale Zwilling seinem realen Pendant gleichen, um tatsächlich rechtskräftige Beurteilungen zu erlauben? Um ein rechtlich belastbares und reproduzierbares Maß an Objektauthentizität zu gewährleisten, entwickeln wir ein Qualitätsmodell, das geodätische Prozessketten und Qualitätsbegriffe zusammenfasst.
 ©
GIH
©
GIH
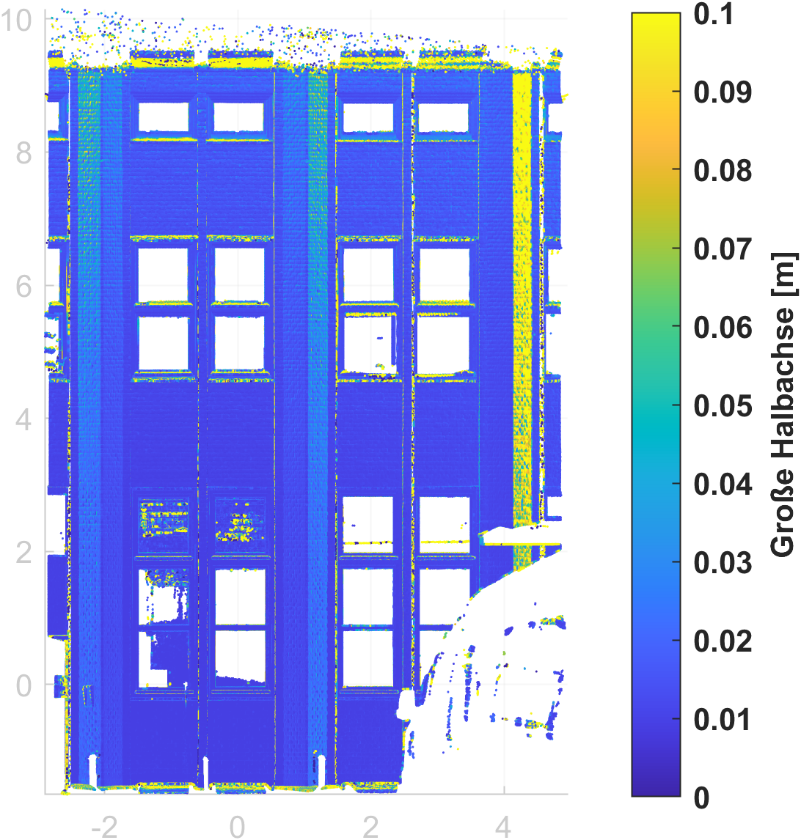
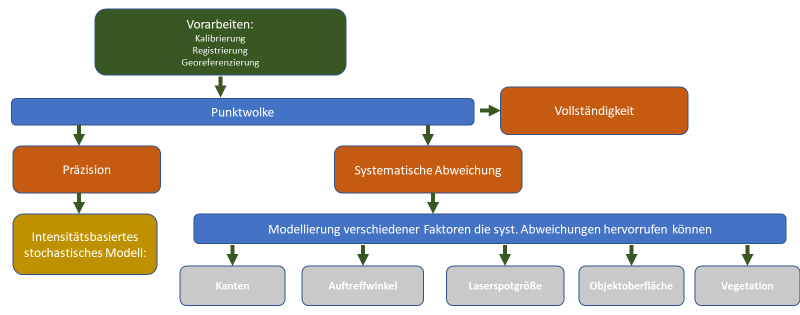
Aktuell bearbeiten wir das Qualitätsmodell für den Laserscanner, mit dem wir die Bauwerke Punkt für Punkt digital erfassen. Um beurteilen zu können, wie genau wir überhaupt mit dem Laserscanner messen (können), müssen wir in unserer Modellierung verschiedene Einflüsse berücksichtigen, die die Messung beeinflussen.
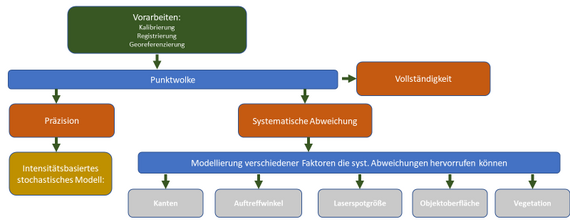
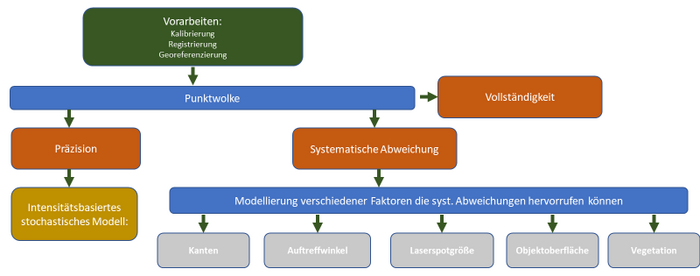
Das fängt bei der Vorbereitung der Messung an: Kleine Unsicherheiten bei der Kalibrierung der Sensoren und der Registrierung bzw. der Georeferenzierung können sich in der Punktwolke fortpflanzen. Damit aus den einzelnen gemessenen Punkten überhaupt ein 3D-Modell werden kann, erhält jeder Punkt Koordinaten, also einen festen Punkt im Koordinatensystem. Mit Hilfe des sogenannten intensitätsbasierten stochastischen Modells können wir die Präzision der Punktkoordinaten berechnen. Dieses liefert für jeden einzelnen Punkt eine Standardabweichung.
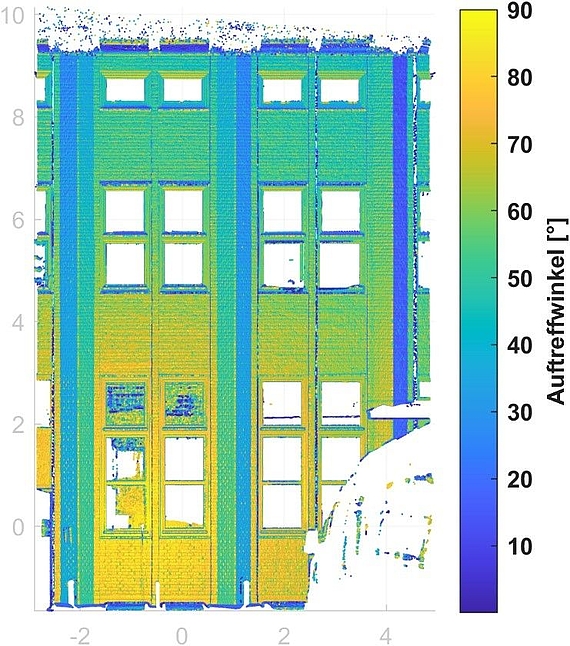
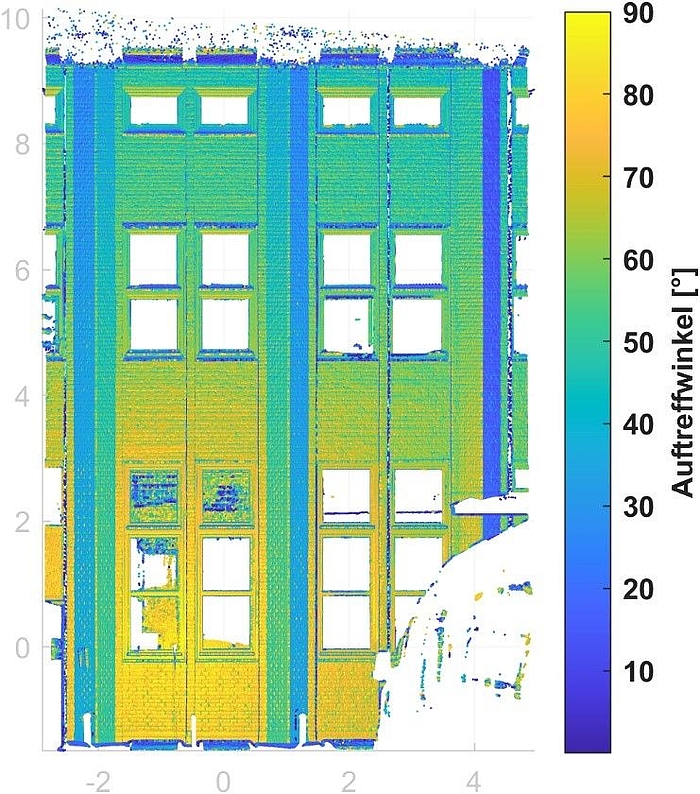
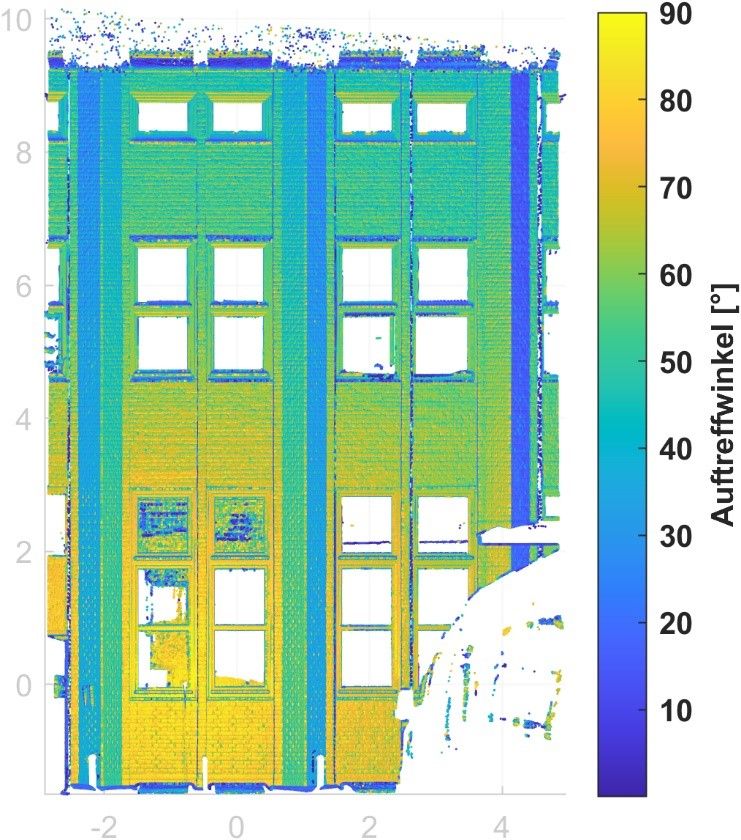
Zusätzlich müssen Einflüsse beachtet werden, die systematische Abweichungen verursachen können. Insbesondere die Distanzmessung ist davon betroffen. Distanzen werden beim Laserscanning über die Zeit bestimmt, in welcher der ausgesendete Laserstrahl am gemessenen Punkt reflektiert wird und wieder am Laserscanner eintrifft. Kleine Auftreffwinkel, große Laserspotgrößen, das Messen von Kanten sowie die Objektoberfläche können zu einer verkürzten oder verlängerten Messung der Distanz führen. Deshalb berechnen wir für jeden Punkt den Auftreffwinkel und die Laserspotgröße und untersuchen, ob es sich um einen Kantenpunkt handelt (Abbildung 3).


 ©
GIH
©
GIH
 ©
GIH
©
GIH
Bis jetzt haben wir die einzelnen Einflüsse separat berechnet. Im nächsten Schritt sollen diese in einem Wert zusammengefasst werden, um eine Beurteilung der Qualität vornehmen zu können. Anschließend erfolgt die Qualitätsmodellierung für weitere Sensoren wie zum Beispiel Kameras und Handscanner.